|
|
เปลี่ยนอัตราแลกเปลี่ยน | ดอกเบี้ยเชิงเดี่ยว | ดอกเบี้ยทบต้น | ความเร็ว | ความเข้มข้น | วิธีสามเหลี่ยม
|
|
การเปลี่ยนอัตราแลกเปลี่ยน
ฝึกการใช้สัดส่วนตรง
ตัวอย่างที่ 1 ให้ 1 ปอนด์ = 1.5 ยูโร จงเปลี่ยน 10 ปอนด์ ให้เป็นสกุลเงินยูโร
|
|
10 ปอนด์ = 1.5 x 10 = 15 ยูโร |
ตัวอย่างที่ 2 จงเปลี่ยน 28 ยูโร เป็นปอนด์
| |
ให้ 1 ยูโร = 1/1.5 ปอนด์ |
| |
28 ยูโร = 1/1.5 x 28 = 18.67 ปอนด์ (ใกล้เคียงเพนนี) |
กฎ คิด 1 หน่วยสำหรับเงินที่ต้องการแลกเปลี่ยน แล้วคูณด้วยจำนวนที่ต้องการแลกเปลี่ยน
|
ดอกเบี้ยเชิงเดี่ยว
เป็นการฝึกเรื่องร้อยละ เป็นการหาดอกเบี้ย จากเงินต้น
| สูตร ดอกเบี้ยเชิงเดี่ยว คือ |
I = PTR
100
|
|
| |
|
|
ซึ่ง
|
|
|
| P = เงินต้น (เงินฝาก หรือเงินลงทุน) |
| T = เวลา (ปี) |
|
|
| R = อัตราดอกเบี้ย (%) |
|
|
ตัวอย่างที่ 1ฝากเงิน 600 บาท เป็นเวลา 8 ปี อัตราดอกเบี้ย 15% จะได้ดอกเบี้ยเท่าไร และ ได้เงินรวมทั้งหมดเท่าไร
|
|
|
|
|
|
|
|
I =
|
|
600 x 8 x 15
100 |
|
R = 15
|
|
|
|
|
| |
ดอกเบี้ย =
|
|
720 บาท
|
|
| |
เงินรวม =
|
|
600 + 720 =
|
1320 บาท |
หมายเหตุ คำถามในบทนี้อาจถามหา I, P, T หรือ R
ก็เพียงแต่แทนค่าในสูตร โดยนำตัวที่โจทย์ต้องการให้หาไว้ซ้ายมือ
ตัวอย่างที่ 2 ฝากเงิน 6,000 บาท เป็นเวลา 1 ปี 6 เดือน ได้รับดอกเบี้ยเป็นเงิน 1,000 บาท ถามว่า อัตราดอกเบี้ยเป็นเท่าไร
|
|
|
|
|
|
|
|
R =
|
|
100 I
PT
|
(R ตัวที่ต้องการหา) |
R = ?
|
|
|
|
|
I = 1000
|
|
|
|
|
| |
R =
|
|
100 x 1000
|
= 11
|
1/9 |
| |
|
|
6000 x 1½
|
|
| |
R=
|
|
11 |
1/9 % |
|
|
|
ดอกเบี้ยทบต้น
กรณีนี้ดอกเบี้ยจะถูกบวกเข้าไปในแต่ละปี คิดเงินรวมในปีแรก แล้วนำไปคิดดอกเบี้ยในปีถัดไป
ตัวอย่างที่ 1 จงหาดอกเบี้ยทบต้นเมื่อเงินฝาก เป็น 900 บาท ในเวลา 3 ปี คิดดอกเบี้ย 5%
| |
ปีที่1 5/100 x 900 = 45 บาท
ปีที่2 5/100 x 945 = 47.25 บาท
ปีที่3 5/100 x 992.25 = 49.61 บาท
|
ดอกเบี้ยทบต้น = 45 + 47.25 + 49.61 = 141.86 บาท
ตัวอย่างที่ 2 จงหาเงินรวม เมื่อฝากครบ 3 ปี
| |
เงินรวม = 900 + 141.86 = £1,041.86 |
สำหรับจำนวนปีมากๆ มีวิธีลัดดังนี้
ใช้ตัวเลขในตัวอย่างที่แล้ว
เงินรวมเมื่อสิ้น ปีที่1 = 105% ของ 900 = 1.05 x 900
สิ้น ปีที่2 = 105% ของปีแรก = 1.05 x 1.05 x 900
นั่นคือในแต่ละปีคูณด้วย 105% = 1.05
ปีสุดท้ายได้เงินรวม = (1.05)3 x 900 = 1,041.86 บาท
(ถ้าใช้เครื่องคิดเลข จะได้)
|
1.05 (ปุ่มยกกำลัง) 3 x 900
^
|
เมื่อจะคิดเวลา 15 ปี ก็เปลี่ยนตัวชี้กำลังเป็น 15
(1.05)15 x 900 = 1,871.04
|
ความเร็ว
ความเร็ว นิยามด้วย ระยะทางที่เดินใน 1 หน่วยเวลา
ตัวอย่างที่ 1 รถยนต์วิ่ง 150 กิโลเมตร กินเวลา 2 ชั่วโมง จงหาความเร็วเฉลี่ย
| |
ใน 1 ชั่วโมง รถวิ่งได้ทาง 150 ÷ 2 = 75 กิโลเมตร |
| |
ความเร็ว = 75 กิโลเมตร ต่อ ชั่วโมง
|
หน่วยของความเร็ว ใช้ กิโลเมตร/ช.ม. หรือ เมตร/วินาที
ข้อสังเกต มักจะใช้หน่วยความเร็วที่กล่าวแล้วในคำถามแต่ละข้อ
ตัวอย่างที่ 2 วัตถุหนึ่งเคลื่อนที่ 30,000 เซนติเมตร ใช้เวลา 0.5 นาที จงหาความเร็วเป็นเมตรต่อวินาที
30000 เซนติเมตร =
0.5 นาที =
ความเร็ว =
|
300 เมตร
30 วินาที
300/30 = 10 เมตร/วินาที
|
|
สูตร ที่ใช้ในเรื่องความเร็ว
|
S = D
T
เมื่อ S แทน ความเร็ว
D แทน ระยะทาง
T แทน เวลา
|
เมื่อใช้สูตรนี้ โจทย์จะให้ค่ามา 2 ค่า เมื่อต้องการหาค่าใด ก็เอาไว้ทางซ้ายมือ แล้วหาตัวแปรตัวที่ 3
ตัวอย่างที่ 3 รถยนต์วิ่งความเร็ว 80 กิโลเมตร/ช.ม. ถ้าใช้เวลา 2 ชั่วโมง จะได้ทางเท่าไร
S = 80
T = 2
D = S x T
D = 80 x 2 = 160 กิโลเมตร
ตัวอย่างที่ 4 รถยนต์วิ่งระยะทาง 300 กิโลเมตรด้วยความเร็ว 60 กิโลเมตร/ช.ม. จะใช้เวลานานเท่าไร
| |
|
|
| S = |
60 |
|
| D = |
300 |
|
| T = |
D |
|
| |
S
|
|
| T = |
300 = 5 ชั่วโมง |
|
| |
60 |
|
|
ความหนาแน่น
ความหนาแน่น คือ มวล ต่อปริมาตร
|
สูตรสำหรับความหนาแน่น
|
|
D = M
|
|
V
|
|
|
เมื่อ M แทน มวล
V แทน ปริมาตร /ลูกบาศก์เซนติเมตร (ซ.ม.3)
|
ตัวอย่างที่ 1 ถ้ามวลของแข็ง 500 กรัม มีปริมาตร 1,000 ลูกบาศก์เซนติเมตร จะมีความหนาแน่นเท่าใด
M = 500
V = 1000
D = 500 = 0.5 กรัม/ลูกบาศก์เซนติเมตร
1000
ตัวอย่างที่ 2 V = 3000ซ.ม.3, D = 0.2 กรัม/ซ.ม.3จงหา M = ?
M = D x V
M = 0.2 x 3000 = 600 กรัม
|
|
วิธีสามเหลี่ยม
ปัญหาที่เกี่ยวข้องกับความเร็ว และความหนาแน่น อาจใช้วิธีสามเหลี่ยม ที่รู้จักกันดี สำหรับการหาความเร็วและความหนาแน่น
ความเร็ว
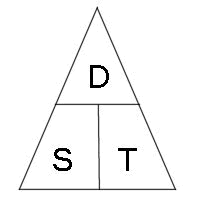
เส้นแนวดิ่ง ในสามเหลี่ยม หมายถึง การคูณ, แนวนอน หมายถึง การหาร
ถ้าทราบค่าของ D, T หรือ S เพียงสองตัว จะทำให้สามารถหาค่าตัวแปรที่เหลือได้
 |
|
D/T = S
D/S = T
S x T = D
|
|
ความหนาแน่น
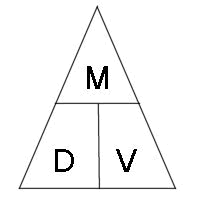
ความหนาแน่น หาได้จากสามเหลี่ยม.
 |
|
M/D = V
M/V = D
D x V = M
|
|
|