Area is the space inside a shape. It is measured by dividing the shape into squares and counting them. If the squares are of side 1cm, then we can use the units cm2.
|
Irregular shapes can be drawn on a grid and the area estimated by counting the squares. Parts of a square need to be added to make a whole square.
|
For example:
Estimate the area of the shape below:
|
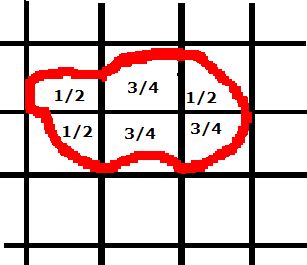 |
Area = 3½ squares |
Regular shapes เช่น รูปสามเหลี่ยม, สี่เหลี่ยมผืนผ้าและรูปว่าว มีสูตรในการหาพื้นที่ดังต่อไปนี้
|
| พื้นที่สี่เหลี่ยมผืนผ้า |
|
|
ตัวอย่าง:
จงหาพื้นที่รูปสี่เหลี่ยมผืนผ้า ABCD. |
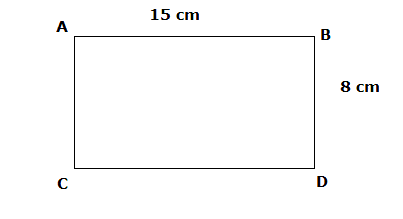 |
พื้นที่=15 x 8= 120 ซ.ม.2 (หน่วยของพื้นที่เป็นตารางเซนติเมตร ซ.ม.2 )
|
| พื้นที่ของรูปสามเหลี่ยม |
|
|
ตัวอย่าง:
จงหาพื้นที่รูปสามเหลี่ยม ABC. |
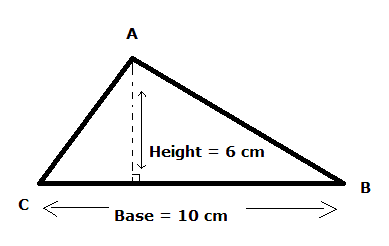 |
พื้นที่=1/2 x 10 x 6= ½ x 60 = 30 ซ.ม.2
|
| (Note: 10 x 60 would give the area of the rectangle standing on BC, the area of the triangle is half this area). |
| |
| พื้นที่สี่เหลี่ยมด้านขนาน |
|
|
| |
ตัวอย่าง:
จงหาพื้นที่รูปสี่เหลี่ยมด้านขนาน PQRS. |
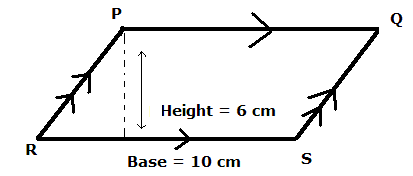 |
พื้นที่ = 10 x 6 = 60 ซ.ม.2
|
| พื้นที่รูปว่าว และขนมเปียกปูน |
| พื้นที่ = ½ (ผลคูณของเส้นทแยงมุม) |
|
ตัวอย่าง
จงหาพื้นที่รูปว่าว ABCD และสี่เหลี่ยมขนมเปียกปูน LMNO. |
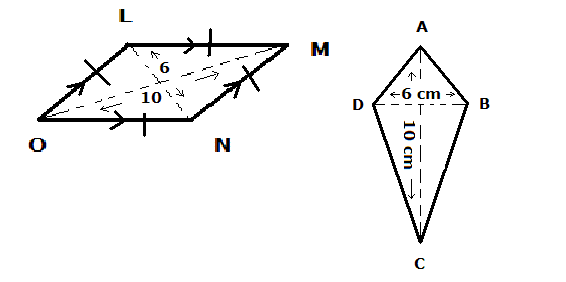 |
พื้นที่ของ ABCD และ LMNO = ½ x 10 x 6 =30 ซ.ม.2
|
| พื้นที่สี่เหลี่ยมคางหมู |
| พื้นที่ = ½(ผลบวกของด้านคู่ขนาน) x สูง |
|
ตัวอย่าง
จงหาพื้นที่รูปสี่เหลี่ยมคางหมู ABCD. |
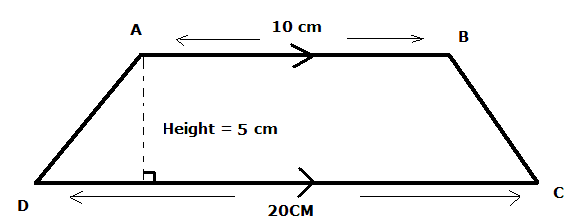 |
พื้นที่ = ½ (10+20) x 5 = ½ x 30 x 5 = 75 ซ.ม.2
|
ข้อสังเกต บางครั้งโจทก์จะกำหนดพื้นที่แล้วให้หาด้าน
|
ตัวอย่าง
จงหาความยาว QR จากรูปสามเหลี่ยมที่มีพื้นที่ 20 ซ.ม.2 |
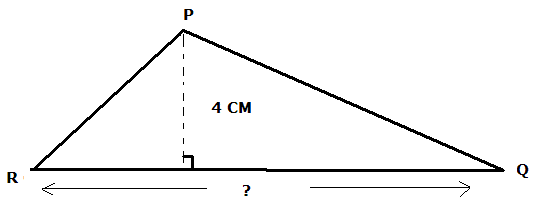 |
20 = ½ x 4 x QR
20 = 2 x QR
QR = 10 ซ.ม.
|
รูปผสม
ในโจทก์บางข้อ ต้องแบ่งรูปทรงออกเป็นรูปเหลี่ยมต่างๆ จึงสามารถจะนำพื้นที่มาบวกหรือลบกัน
|
ตัวอย่าง
จงหา ก.) พื้นที่ทั้งหมด และ ข.) พื้นที่แรเงา |
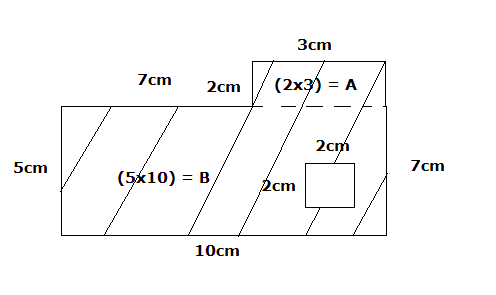 |
ก.) พื้นที่ทั้งหมด = พื้นที่ A + พื้นที่ B
=(2x3) + (5x10)
= 6+50
= 56 ซ.ม.2 |
ข.) พื้นที่แรกเงา = 56 – (2x2)
= 52 ซ.ม.2 |
| |